一般相対性理論についてAIから学ぶ

はい、colorful beansです。
今回の記事は一般相対性理論についてです。

前回までに続いて宇宙の創造、仕組みを理解、学ぶうえで必ず必要となる理論ですね。
ちょっとした気持ちで書き始めた宇宙についての記事ですが、ここまで回数・分量になるとは・・・^^;

では、はじめましょう！　
今回のAI　チャットGPTを活用しておりますので、事実と異なる点や誤字脱字は予め理解したうえで読んでくださいね。

一般相対性理論とは
一般相対性理論の概要と歴史的な背景について
等価性の原理について解説
1. 弱い等価原理について
2. 強い等価原理について
曲率の原理（Principle of Curvature）について解説
リーマン幾何学について解説
測地線の方程式について
一般相対性理論の基本概念
アインシュタイン方程式について解説
時空連続体の歪みについて
宇宙と一般相対性理論
一般相対性理論の実証と重要な実験・観測結果
後書き

一般相対性理論とは

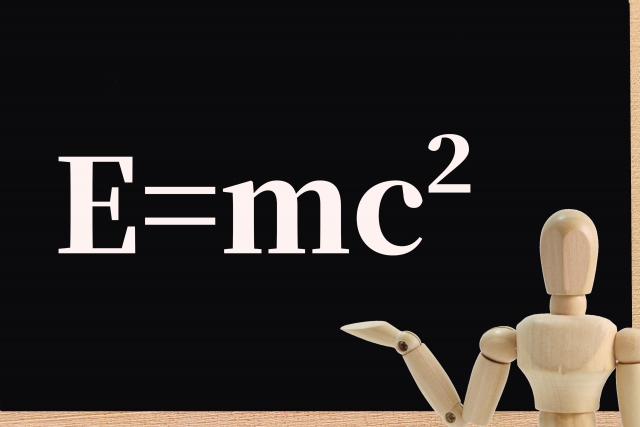
一般相対性理論は、アルベルト・アインシュタインによって提唱された物理学の理論で、重力の仕組みは実は質量のある物質の存在が時空間を歪めることにより物体に力が働いているようにみえる、という革新的で美しい微分幾何学的な理論です。一般相対性原理と一般共変性原理および等価原理を理論的な柱とし、リーマン幾何学を数学的土台として構築された古典論的な重力場の理論であり、測地線の方程式とアインシュタイン方程式（重力場の方程式）が帰結である。

一般相対性原理と一般共変性原理および等価原理
リーマン幾何学
測地線の方程式
アインシュタイン方程式（重力場の方程式）
時空連続体の歪み

など重要な要素がいくつもあります。

一般相対性理論の概要と歴史的な背景について

一般相対性理論は、アルベルト・アインシュタインによって1915年に提唱された物理学の理論です。それ以前の物理学では、重力はニュートンの万引力の法則によって説明されていましたが、アインシュタインは新たな理論を提案しました。

一般相対性理論の背景には、アインシュタインが特殊相対性理論（1905年）を発展させる過程があります。特殊相対性理論では、時間や空間が統一的な優位である時空として捉えられ、光速度がこれにより、時間や空間の概念が従来のニュートン力学からは異なるものとして再定義されました。

アインシュタインは、特殊相対性理論が高速度での物体の挙動を繰り返し、重力を説明するための理論が不足していると考えました。このことによって重力が生じるという新しい理論を構築しました。

このアインシュタインのアイデアに基づく一般相対性理論は、1915年に最初の形で発表されました。彼は重力を質量やエネルギーが存在する時空の曲率として捉え、物体や光がこの曲がった時空の中でで運動することによって重力の効果が起こることを示しました。

一般相対性理論は、初期の提案後に発展を実現し、数学的に厳密な形状で表現されました。その後の実験や観測結果が、一般相対性理論の予測と一致することが確認され、理論特に、太陽の重力によって光が曲がることが観測されたことや、重力赤方偏移と呼ばれる現象が観測されたことは、一般相対性理論の成功例とされているます。

一般的な相対性理論は、宇宙の進化や重力に関する考慮のための重要な意見となっています。

一般相対性理論は、重力を「時空の幾何学的な曲率」として解釈します。質量やエネルギーが存在すると、それらは時空を曲げる効果を持ちます。この曲がった時空において、物体や光はまっすぐですな直線（地平線）ではなく、曲線を描いて運動することになります。この運動が我々にとっては重力として観測される現象です。

一般相対性理論の重要な特徴は、時間と空間の関係も変えることです。重力場の中では、時間の経過や物の運動速度は他の場所や重力場の影響によって異なる速度で進むことまた、重力場の強さは質量やエネルギーの分布によって決まるため、重力場は物体同士の相互作用の結果として現れます。

一般相対性理論は、多くの実験や観測結果によって裏られています。特に、太陽の周囲を公転する惑星の歩道や重力レンズ効果、時空の歪みを持つブラックホールの存在など、これらの現象が一般的相対性理論の予測と一致していることが観測されています。

一般相対性理論は、物理学重要な理論の一つであり、現代の宇宙論や天体物理学の研究においてはかなりの限界となっています。その深い理解と応用は、私たちの宇宙の構造や進化、重力に関する謎を解明する上で重要な役割を果たしています。

等価性の原理について解説

等価性の原理（Equivalence Principle）は、一般相対性理論において重要な概念の一つです。この原理は、重力と加速度の間に等価性があるという考えを考えています。

等価性の原理は、アインシュタインが重力の本質を理解するために導入しました。原理の主要な内容は以下の通りです。

一様加速度の等価性：無重力自由放置状態と一様な加速度による非重力状態は、物理的に等価であるとされます。重力のない空間で加速されている物体は、同じ物理的な現象を経験します。

重力場の中の一様性：小さな領域内での重力場は一様とみなせるという考えです。この原理によれば、特定の領域内での重力場は、一様な重力場とみなして扱うことこれは、同じような重力場の中での実験や観測結果は、その領域内のどの場所で行っても同じ結果を考えるということを意味します。

等価性の原理によれば、物体が重力場中に存在するとき、その物体は等価的な加速度を経験していると解釈することができます。物体自体が静止している状態で重力がかかっている場合と等価であるとされます。

この等価性の原理は、一般相対性理論の基礎となる重要な概念です。アインシュタインは、等価性の原理を用いて、重力を曲がった時空の結果として説明しました。、その周りの時空が歪むことによって物体は重力の影響を受けます。この歪んだ時空の中で物体や光が運動することによって、重力現象が起こるのです。

等価性の原理は、重力と加速度の関係を示すだけでなく、一般相対性理論における重要な予測をもたらしました。例えば、光が重力場を通過する際に曲がる現象や、時空の曲率による時間の遅れ（時間膨張）など価性の原理に基づいて説明されます。

以上が等価性の原理についての解説です。

弱い等価原理について

弱い等価原理（Weak Equivalence Principle）は、重力と慣れという性質の間に等価性がある原理です。この原理によれば、質量の異なる物体が同じ加速度で運動するとき、それらは重力とは独立して運動しますもしよろしければできます。

具体的には、弱い等価原理は以下のような主張をします：

自由落下の等価性：無重力の状態（自由落下）と、重力下での質量の異なる物体等速度運動は、物理的に等価であるとされます。その中で自由に離脱する場合、それらは同じ加速度を持って離脱すると考えられます。

質量による影響の欠如：弱い等価原理によれば、物体の質量がその運動に影響を与えることはありません。

エトヴェシュ・ロラーンドによる 1908年の実験が有名で、同じ質量の二つのおもりを天秤にかけ、重力加速度と地球の回転による加速度の違いで生じる天秤のねじれを利用して等価原理を検証しようというもので、その結果は、10−9 の精度であった。

強い等価原理について

強い等価原理（Strong Equivalence Principle）は、重力と慣性の完全な等価性を主張する原理です。この原理であれば、重力場内の任意の小さな領域では、その領域内の物理法則は重力の存在に有利、特殊対立性理論の優位で説明できます。

強い等価原則は以下のような主張を含んでいます：

自由残留の等価性：強い等価原則は、自由残留する物体と重力のかかってない非重力状態での物体の運動が、物理的に等価であると主張します。その中でも特殊相対性理論に運動するものとされます。
全ての物理現象の等価性：強い等価原理は、重力場中の全ての物理現象が重力の存在に依存せず、特殊相対性理論によって説明できると主張します。重力の効果がある場合でも、その効果は曲がった時空によるものであり、特殊相対性理論の法則に沿った物体の運動や相互作用に影響を考慮するものではないとされます。
ローカルな等価性：強い等価性原理は、等価性がローカルな性質であると主張します。や時間スケールが大きくなる場合、重力場の勾配や曲率が考慮される必要が出てくるため、等価性が成り立たなくなることがあります。

強い等価原理は、アインシュタインの一般相対性理論の基礎となっています。この原理によって、重力と慣性の完全な等価性が示されるため、物体や光が曲がった時空内で運動することや、重力場における時間の古いなどが説明できるのです。

強い等価原理は、重力の本質を理解の上で重要な役割を果たしています。重力は、質量やエネルギーによって時空を曲げる力として理解されます。幾何学的な概念として表現し、物体や光の運動を曲がった時空の中で行うことが可能になりました。

強い等価原理は、実験や観測によっても裏付けられています。例えば、重力場内の光の曲がり具合の観測や、物体自由自在の行動の観察など、等価性の原理と一致する結果を示しています。

一般相対性理論は、強い等価原理を基礎として重力を説明し、宇宙の大規模構造やブラックホールなどの現象を予測するなど、広範な物理学分野で応用されている。学や宇宙物理学の基礎として重要な理論です。

アインシュタインによる一般相対性理論の構築と強い等価原理の導入は、物理学の進歩において重要な変革点となりました。

曲率の原理（Principle of Curvature）について解説

曲率の原理（Principle of Curvature）は、一般相対性理論において重要な概念の一つです。この原理は、重力場が物体や光線の通り道を曲げるという現象を説明します。

一般相対性理論では、重力場を曲がった時空として記述します。この時空の曲率は、物体の質量やエネルギーによって決定されます。曲率の原理によれば、物体や光線は、曲がった時空で際に曲率に応じて運動することになります。

具体的には、曲率の原理は以下のような主張を含んでいます：

時空の歪みによる運動：曲率の原理によれば、物体や光線は、曲がった時空の中で運動する際に、その時空の曲率に従った経路配置とされます。曲がるため、物体や光線は直線的な経路ではなく、曲がった経路をたどることになります。
時空の曲率と物体の運動：曲率の原理によれば、質量やエネルギーを持つ物体が存在すると、その周りの時空が曲がることになります。引かれるような運動をすることになります。この運動は、物の質量や速度によって決まります。

曲率の原理は、重力場が物体や光線の通り道を曲げる現象を説明するために非常に重要です。実際の観測や実験結果も、曲率の原理と一致しており、重力場によって物体の軌道が曲がる現象や、重力レンズ効果（光線が重力場によって曲がる現象）などが観測されています。

一般相対性理論は、曲率の原理を基礎として、重力を時空の曲がりによって行う理論です。これによって、宇宙の構造やブラックホールなどの重力現象を解明することが可能になりました。

以上が曲率の原理についての解説です。曲率の原理は、一般相対性理論の基礎です。

リーマン幾何学について解説

リーマン幾何学は、19世紀にドイツの数学者ベルンハルト・リーマンによって発展された数学の分野です。リーマン幾何学は、ユークリッド幾何学における平面や直線などの図形に限定されない、より一般的な幾何学理論を提供します。

ユークリッド幾何学では、平面上の点や直線の性質や関係を研究しますが、リーマン幾何学では、曲面や高次元空間などのより一般的な幾何学的な対象を考察します。直線の概念を曲線に一般的に変更し、平面を一般的な曲面に拡張します。

リーマン幾何学の基本的な要素は、以下のようになります：

曲面：リーマン幾何学では、平面に限定せず曲面を対象とします。曲面は、平面と異なる曲率や曲線の性質を持ちます。例えば、球面やトーラスなどの曲面の例です。

測地線：リーマン幾何学においては、直線の概念を曲線に一般化したものを測地線と呼びます。測地線は、曲面上の最短距離や最速経路として定義されます。

曲率：リーマン幾何学では、曲面の曲がり具合を表す曲率が重要な概念です。曲率は、曲面上の点における測地線の曲がり具合を表します。曲率が大きい曲面はより曲がっていると言えます。

リーマン幾何学は、ユークリッド幾何学とは異なる幾何学的な概念や性質を研究するため、数学や物理学の幅広い分野で応用されています。の表現にはリーマン幾何学が利用されています。また、地球の地形や曲面の性質を理解する地理学や地球科学の分野でも重要な役割を果たしています。

測地線の方程式について

測地線は、リーマン幾何学において曲面や多様体上の最短距離や最速経路を代表します。測地線は、一般相対性理論における時空の粒子や光線の運動を優先するためにも重要ですな概念です。

測地線の方程式は、曲面多様体の曲率やメヤトリック（距離の概念）に関連しています。具体的には、以下のような方程式で表されます。

リーマン幾何学における測地線の方程式： 2次元曲面上の場合（平面や球面など）では、測地線の方程式は通常の微分方程式で表されます。具体的な形式は、曲面のメトリック（距離の概念）一般的には、測地線の不足に関する2階微分方程式として表されます。

3次元以上の多様体や一般相対性理論における時空では、測地線の方程式はさらに複雑になります。
ここでは、一般的な曲率テンソルや接続係数に基づいた微分方程式として表されます。

測地線の方程式の解決は、与えられた初期条件（位置と速度）によって決まります。初期条件を慎重に、測地線の形状や経路を特定することができます。

測地線は、最短距離や最速経路を表すため、重力場中の物体や光線の運動のために重要な役割を行っています。沿って運動されます。重力場が曲がった時空を生成するため、物体や光線も曲がった経路をたどることになります。

測地線の方程式を解析的に求めるためには、特定的な曲面や多様体のメトリックや接続係数に関する情報が必要となります。これは通常、リーマン幾何学や一般相対性理論の研究において数学的なものです手法や計算技術を用いて解析されます。

一般的に解析的に、測地線の方程式はような非形の微分方程式であり、解決を求めることは難しい場合があります。ただし、特定の場合や簡単な曲面に関しては、解析的な解決が得られることもあります。

また、数値的な手法や計算シミュレーション機を置くことで、地線の方程式を数値的に理解することも可能です。これによって、具体的な初期条件や曲面の性質を測って、測地線の経路や形状を計算することができます。

測地線の方程式は、宇宙論やブラックホールの研究など、一般相対性理論の重要な応用分野で広く使用されています。これによって、重力場中物体や光線がどのように運動するのか、観測結果と理論の予測を比較することで、宇宙の構造や運動の法則を踏まえることができます。

以上が測地線の方程式についての解説です。地線はリーマン幾何学や一般相対性理論において重要な概念であり、宇宙や重力場の研究においては当然の役割を果たしています。

一般相対性理論の基本概念

一般相対性理論の重要な概念について説明します。例えば、時空の計量（メトリック）、重力場の方程式（アインシュタイン方程式）、クリストフェル記号などです。物理的な現象や観測結果と関連しているのかを解説。

時空の計量（メトリック）: 時空の計量は、一般相対性理論において重要な役割を果たします。メトリックは、時空の距離や時間の慎重を定義し、時空の幾何学的な性質を表現します。一般相対性理論では、時空は一般的に非ユークリッド幾何学的な性質を持つため、メトリックは通常、テンソルとして表されます。
重力場の方程式（アインシュタイン方程式）: アインシュタイン方程式は、重力場の振る舞いを表現するための方程式です。これは、時空の曲率とエネルギー・運動量の関係を書きます。アインシュタイン方程式によって、物体やエネルギーが時空の曲率をかえし、それによって物体や光の運動が変化します。具体的には、左辺のリッチテンソル（時空の曲率の一部）とスカラー曲率と、漸くのエネルギー・運動量テンソルの関係が等しくアインシュタイン方程式は、時空の曲率が物体やエネルギーによって決まることを示しており、これによって重力の考え方や行動を理解することができます。
クリストフェル記号: クリストフェル記号は、時空の接続性を表現するために使用される量です。一般相対性理論では、時空は曲がった非ユークリッド幾何学的な性質を持ちます。クリストフェル記号は、時空の曲率や物体の運動に関連する重要な情報を提供します。クリストフェル記号は一般相対性理論において重要な概念であり、時空の曲率や物体の運動に関する理論や計算において重要な道具となっています。

アインシュタイン方程式について解説

アインシュタイン方程式は、アルベルト・アインシュタインによって一般相対性理論の基礎となる重力場の方程式として提案された方程式です。これは、重力場曲率とその曲率に対するエネルギー・運動量の関係を表現しています。

アインシュタイン方程式は、重力場を時空の幾何学的な曲率に定めることで、物体や光線の運動、時空の構造や展開、宇宙の進化などをのために使用されます。

アインシュタイン方程式は次の形式で表されます：

R_{\mu\nu} – \frac{1}{2}g_{\mu\nu}R = \frac{8\pi G}{c^4}T_{\mu\nu}

ここで、R_{\mu\nu} はリッチテンソル（曲率テンソルの一部）、g_{\mu\nu} は時空のメトリックテンソル（時空の計量を表すテンソル）、R はスカラー曲率、G は万有引力定数、c は光速、T_{\mu\nu} はエネルギー・運動量テンソルです。

この方程式は、左辺の曲率と先ほどのエネルギー・運動量の密度の関係を表しています。学的な曲率は、物体やエネルギーの存在分布やによって決まるということを表しています。

アインシュタイン方程式は非線形の微分方程式であり、一般相対性理論における重力現場の行動を捉えるための基本的な方程式となります。この方程式の解析的な解決は一般に困難であり、特殊な条件や対称性を仮定することで解析が得られる場合もあります。

アインシュタイン方程式は、宇宙の大規模構造、ブラックホールや重力レンズ現象、宇宙膨張や宇宙背景放射など、重力現象や宇宙の進化に関する理論的な予測や観測的な検証に広く使用されています。

重力場の方程式としてのアインシュタイン方程式は、一般相対性理論における重要な基礎であり、重力の理解や予測に定めな役割を果たしています。考慮影響が曲率として現れ、その曲率はエネルギー・運動量の分布に依存しています。

アインシュタイン方式の解析的な解決を求めることは一般に困難ですが、特定の場合や対称性を持つ場合には解析的な解決が得られることがあります。な質量分布に対するシュワルツシルト解があります。これは、ブラックホールの解であり、ブラックホールの存在や特性を理解するための基礎となっています。

また、アインシュタイン方程式は数値的な手法や計算機シミュレーションを用いても解くことが可能です。これによって、特定の初期条件や物体の分布を与えて、重力場の時間的な進化や物体の運動を数値これによって、ブラックホールの衝突や重力波の発生など、重力場の複雑な現象を研究することができます。

アインシュタイン方程式は、一般相対性理論の重要な結果として、重力の本質を認識するための理論的な優位性を提供しています。これによって、重力場が物体やエネルギーによって曲がり、時空の幾何学が変化するさらに、アインシュタイン方程式は宇宙の進化や大規模構造の形成、宇宙背景放射の起源など、宇宙全体のダイナミクスを確保するためにも使用されます。

アインシュタイン方程式は、重力の理解や宇宙の研究において基本的な役割を果たす重要な方程式であり、その解析や応用は現代物理学にとって重要な課題の一つです。

時空連続体の歪みについて

時空連続体の歪みは、一般相対性理論において重要な概念です。一般相対性理論では、重力は時空の曲率によって表現されます。これは、物体やエネルギーの存在によって時空が歪むことを意味します。

一般相対性理論では、通常の3次元の空間に加えて、時間を含んだ4次元の時空が考慮されます。この時空は連続的な曲面として扱われ、物体やエネルギーの存在によって歪むことがあります。この歪みは、時空の曲率として表現されます。

時空の曲率は、物体やエネルギーの存在によって決まります。一般相対性理論では、物体やエネルギーが時空に与える影響が曲率として現れ、時空の幾何学的な性質を変化させます。これによって、物体や光の運動に影響が及びます。

具体的には、質量やエネルギーの存在によって時空が歪むと、物体は通常の直線運動ではなく、曲がった経路を辿ることになります。これを「測地線の曲率」と呼びます。また、光も時空の曲率によって曲がるため、重力の影響下では光の進路が変わることがあります。この現象を「重力レンズ効果」と呼びます。

時空の歪みは、一般相対性理論の基本的な概念であり、重力の理解や予測に不可欠な役割を果たしています。これによって、重力場の性質や物体の運動、宇宙の進化などを理解することができます。また、重力波と呼ばれる時空の歪みが波の形式で伝播する現象も予測され、その観測によって重力場の情報が得られるようになりました。

時空連続体の歪みは、一般相対性理論の中核となる概念であり、重力の本質を捉えるための理論的な枠組みを提供しています。

宇宙と一般相対性理論

宇宙における一般相対性理論の応用は、私たちが観測している宇宙の構造や進化を理解する上で重要な役割を果たしています。以下に、一般相対性理論の応用の一部を紹介します。

宇宙の大規模構造: 一般相対性理論は、宇宙の大規模構造の形成と進化を説明する上で重要です。宇宙は大規模なスケールで構造化されており、銀河団や超銀河団といった巨大な構造が形成されています。一般相対性理論は、重力の作用によって物体が集まり、宇宙の大規模な構造が形成されるメカニズムを提供します。
宇宙膨張: 一般相対性理論は、宇宙の膨張を説明するための理論的な枠組みを提供します。観測によって明らかになった宇宙の膨張は、一般相対性理論の予言の一つです。アインシュタインの方程式によれば、宇宙はエネルギーや物質の存在によって時空が曲がり、その曲率によって宇宙の膨張や収縮が起こることが示されます。
ブラックホール: ブラックホールは、一般相対性理論の重要な予言の一つです。ブラックホールは、質量が非常に大きくなり、その重力が光さえも逃すことのできない領域を形成する天体です。アインシュタイン方程式によってブラックホールの存在と性質が予言され、観測によってその存在が確認されました。
重力レンズ: 重力レンズ効果は、一般相対性理論の重要な応用の一つです。重力は光の進路を曲げるため、重力場の存在によって遠くの光が曲がり、観測者にとっては遠くの天体の像が拡大・歪曲される現象です。これによって、遠くの天体の位置や性質を推定することができます。

これらの現象や応用において、一般相対性理論は以下のように説明されています。

宇宙の大規模構造: 一般相対性理論では、重力の作用によって物体が集まり、宇宙の大規模な構造が形成されると考えられています。物体の質量やエネルギーが時空の曲率を生み出し、他の物体を引き寄せるため、銀河や銀河団などの構造が形成されます。
宇宙膨張: 一般相対性理論では、アインシュタイン方程式によって宇宙の膨張が説明されます。宇宙は初期のビッグバンから現在まで膨張を続けており、その膨張速度は宇宙のエネルギーや物質の分布によって決まります。重力によって時空が曲がるため、遠くの銀河は私たちから遠ざかるように見えます。
ブラックホール: 一般相対性理論では、ブラックホールは質量が非常に大きくなり、その重力が光さえも逃せない領域を形成するとされます。ブラックホールは重力が非常に強いため、周囲の物体や光が吸い込まれてしまいます。これは、質量が集中して時空が強く曲がる結果として現れます。
重力レンズ: 重力レンズ効果は、重力によって光の進路が曲がる現象です。一般相対性理論では、質量が存在すると時空が歪み、光はその歪んだ時空を通る際に曲がることが説明されます。重力レンズ効果は、遠くの天体の光が曲がり、私たちの観測において遠くの天体の像が拡大・歪曲される現象として観測されています。

これらの現象や応用は、

一般相対性理論では、時空の曲率を表すために「メトリック」と呼ばれる量が使用されます。メトリックは、時空の距離や時間間隔を定義し、時空の計測や物体の運動を記述します。アインシュタイン方程式は、メトリックと物体やエネルギーの分布との関係を表す方程式であり、時空の曲率を決定します。

さらに、クリストフェル記号は、時空の曲率に関連する量です。クリストフェル記号は、メトリックの微分によって求められ、時空の曲率や物体の運動に関する情報を提供します。物体が重力場の中で自由に運動する際に、クリストフェル記号は物体の運動方程式に現れ、重力の影響を示します。

また、測地線方程式も重要な概念です。測地線は、時空上の最も短い経路を表し、物体や光の運動を記述します。一般相対性理論では、時空の曲率によって測地線が曲がるため、物体や光の運動は通常の直線ではなく、曲がった経路を辿ります。測地線方程式は、時空の曲率と物体の運動を関連付ける方程式であり、物体の運動を予測するために使用されます。

これらの基本的な概念や方程式を組み合わせることで、一般相対性理論は宇宙の大規模構造や宇宙膨張、ブラックホールの性質、重力レンズ効果などの現象を説明し、観測結果と一致させることが可能となります。一般相対性理論は、重力の本質を理解し、宇宙の進化や構造の形成について深い洞察を提供する重要な理論となっています。

一般相対性理論の実証と重要な実験・観測結果

一般相対性理論は、多くの実験や観測結果によって実証されてきました。以下に、一般相対性理論を支持する重要な実験と観測結果をいくつか紹介します。

太陽光の重力による曲がり（1919年の日食観測）: 1919年に行われたエジントン観測は、一般相対性理論の初期の実証の一つです。太陽の重力によって光が曲がるというアインシュタインの予言を確かめるため、日食の際に太陽の周りの星の位置を観測しました。その結果、星の位置が太陽の周りでわずかにずれていることが観測され、一般相対性理論が実証されたとされました。
重力赤方偏移（1960年代以降の観測）: 一般相対性理論では、重力場の中で光の波長が伸びることが予言されています。これは、重力場によって光がエネルギーを失い、波長が赤くずれる現象です。実際に、地球から遠くの銀河やクエーサーからの光が観測された際に、その光の波長が赤くずれていることが確認されています。これは、重力による光の赤方偏移として一般相対性理論の予言を支持する重要な観測結果です。
ダブルパルス型ニュートン望遠鏡（1970年代の観測）: ダブルパルス型ニュートン望遠鏡は、重力場中を通る光の赤方偏移を観測するために設計されました。この望遠鏡を用いて行われた観測では、重力場中を通った光の赤方偏移が予測通りの結果を示し、一般相対性理論の妥当性を裏付けるものとなりました。
パルサーの軌道崩壊: パルサーは非常に正確なパルス信号を発する天体であり、連星系でのパルサーの観測を通じて一般相対性理論が確かめられています。連星系の中のパルサーの軌道は時間とともに縮まっていくはずですが、その軌道崩壊の速さが一般相対性理論と予測される値と一致していることが観測されました。
ブラックホールの存在の確認: 一般相対性理論ではブラックホールは重力の強い領域であり、周囲の物体や光を捕らえることが予言されています。観測では、ブラックホール候補天体の周りに物質が集まり、その周囲からの光が捕らえられていることが確認されています。また、重力波観測によってもブラックホールの存在が間接的に検出され、一般相対性理論の予測と一致していることが示されています。
宇宙膨張の観測: 宇宙膨張は一般相対性理論の重要な予言の一つです。観測では、遠くの銀河からの光の赤方偏移を測定することで、宇宙が膨張していることが確認されています。この観測結果は、一般相対性理論に基づいて宇宙のダイナミクスを説明する重要な証拠となっています。

これらの実験や観測結果は、一般相対性理論の妥当性を支持し、理論が宇宙や重力に関する現象を正確に説明していることを示しています。一般相対性理論は、その予言が観測や実験によって裏付けられていることから、現代物理学の基盤となる重要な理論と位置づけられています。